Цель урока: изучить алгоритм нахождения наибольшего общего делителя двух чисел.
Пример 1. Алгоритм Евклида для вычисления наибольшего общего делителя (НОД) двух натуральных чисел приведён ниже.
var
a, b: integer;
begin
write(' a = ');
read(a);
write(' b = ');
read(b);
while a <> b do
if a > b then
a := a - b
else
b := b - a;
writeln ('НОД = ', a);
end.Повторение
Операция div осуществляет целочисленное деление, при котором остаток от деления отбрасывается. Операция mod вычисляет остаток от деления
| Название | Запись в Pascal | Пример |
| деление нацело | div | a div b |
| остаток от деления | mod | a mod b |
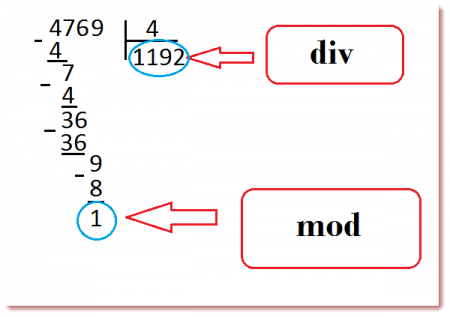
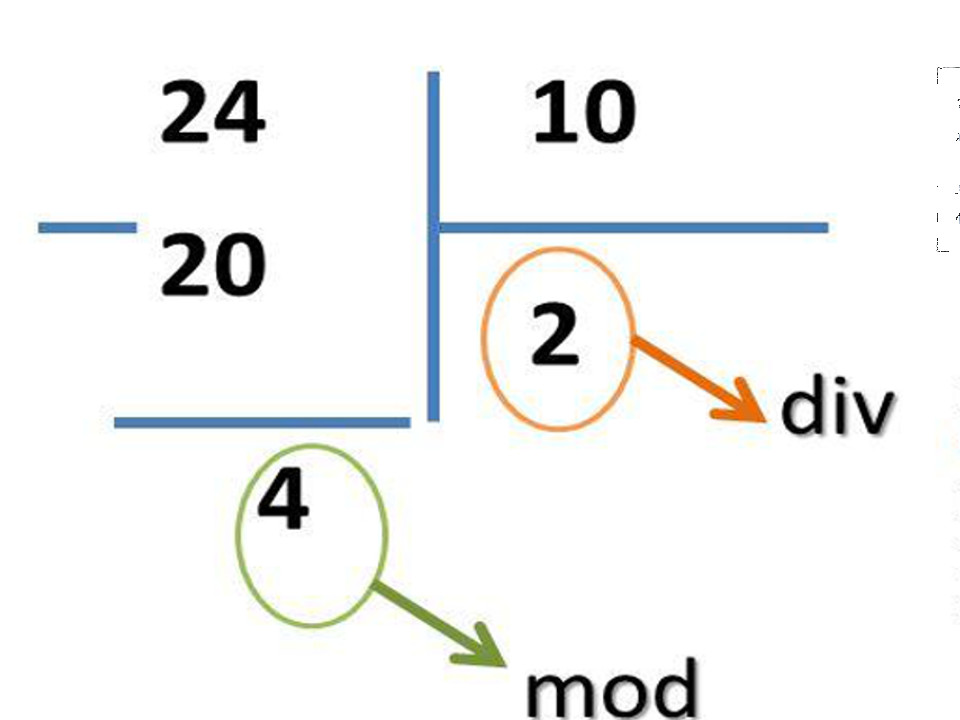
Результат операций div и mod для различных чисел
| a | b | a div b | a mod b |
| 17 | 3 | 5 | 2 |
| -17 | 3 | -5 | -2 |
| 17 | -3 | -5 | 2 |
| -17 | -3 | 5 | -2 |

Задания по теме урока
Задание 1. Напишите программу, которая считает сумму цифр введенного числа.
Указание: обратите внимание на Пример 1 из Урока 24
Задание 2. Напишите программу, которая находит НОК двух чисел. Связь НОК и НОД приведена ниже:
НОК (a, b) = a·b:НОД (a, b)
Задание 3. Дано четырехзначное число N. Напишите программу, которая проверяет, являются ли симметричные части числа одинаковыми числами. Например, 1212 — является, 1235 — нет.
Указание: обратите внимание на операторы mod и div
Дополнительное задание
Дано натуральное число n. Выведите номера разрядов, в которых стоят цифры, кратные 3, или сообщение, что таких цифр нет.

Домашнее задание
§ 19.6 учебного пособия, ответить на вопросы
Форма отправки решений
Форма видна только зарегистрированным пользователям.
