Цель урока: создать модель полета тела, брошенного под углом к горизонту.
Постановка задачи (этап 1)
Задача. Под углом 60° к горизонту и начальной скоростью 30 м/с брошен камень. Сопротивление воздуха не учитывается.
Вопросы:
- Как далеко от места бросания камень упадет?
- Сколько секунд камень будет находиться в полете?
- Какова наибольшая высота взлета камня?
- Как скоро от начала полета будет достигнута наивысшая точка полета?
Выбор плана создания модели (этап 2)
Объектом исследования является положение в пространстве летящего тела в зависимости от времени.
Определенно ясно, что камень при данных начальных условиях действительно должен полететь.
Для создания модели потребуются специальные знания из курса физики и математики. Устное решение задачи невозможно.
Для решения задачи нужно строить документальную математическую модель задачи (уравнения, формулы).
Дальнейшее моделирование возможно двумя путями. Решение математической задачи можно получить в виде формулы (аналитическое решение). Второй путь связан с построением компьютерной модели (расчетное решение).
Будем строить компьютерную модель с помощью электронных таблиц, рассчитывая для разных моментов времени удаление и высоту полета камня.
Таким образом, получаем этапы создания модели:
- 3а — создание документальной математической реализации модели.
- 3б — создание компьютерной реализации модели.
Создание документальной математической реализации модели (этап 3а)
В вертикальной плоскости полета камня зададим прямоугольную систему координат с началом в точке вылета.
Схема представлена на рисунке
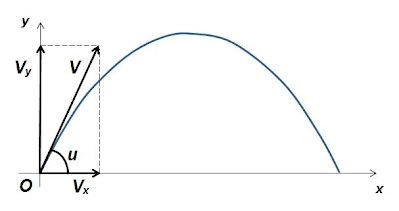
Начальная скорость v (м/c) разлагается на составляющие vx и vy по углу бросания u в градусах:
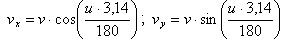
Положение тела в полете определяется парой координат x(t), y(t). Зависимость координат от времени t (с) описывается формулами:
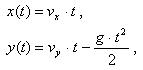
где g = 9,81 — ускорение свободного падения, т.е.
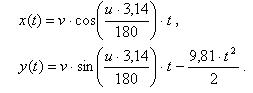
Положение камня в полете будем рассматривать в отдельные моменты времени t0, t1, t2 и т.д. Пусть начальный момент t0 равен 0, а последующие моменты отстоят друг от друга на одну и ту же величину dt, называемую шагом времени. Зададим dt = 0,2 c.
Создание компьютерной реализации модели (этап 3б)
Используем табличную схему модели в электронных таблицах.
В первую строку рабочей таблицы введем название «Модель полета тела».
Исходными данными для задачи являются начальная скорость (30 м/с), угол бросания (60 град.) и шаг времени (0,2 с).
В расчетной таблице в столбцах будем отображать: время с начала процесса (столбец Время), координату-удаление (столбец x(t)) и координату-высоту (столбец y(t)). Модель получит вид, приведенный на рисунке
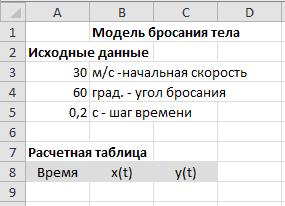
Вводим данные в первую строку расчетной таблицы:
A9: 0 В9: 0 С9: 0
Вторая строка расчетной таблицы — формульная:
A10: =A9+$A$5
В10: =$A$3*COS($A$4*3,14/180)*A10
C10: =$A$3*SIN($A$4*3,14/180)*A10–9,81*A10^2/2
Абсолютные адреса в формулах введены для обеспечения последующего копирования формул.
Следующие 35 строк расчетной таблицы, включая строку 45 рабочей таблицы, заполняем вниз содержимым блока A10:C10.
Расчетную таблицу можно дополнить диаграммой.
Выделяем в расчетной таблице блок B9:C45 и вставляем на свободное место рабочей таблицы диаграмму (Точечная с гладкими кривыми и маркерами). Легенду можно удалить.
Проверка адекватности модели (этап 4)
Адекватность модели проверяется рассчитанными данными. Для 1 сек полета удаление равно 15,01379067 м, а высота — 21,06779518 м.
Модель адекватна реальному процессу только с допущением об отсутствии сопротивления воздуха и для положительных значений координат. Когда координата (высота) становится отрицательной, модель становится неадекватной (тело находится ниже уровня земли).
Получение решения задачи с помощью модели (этап 5)
Для ответа на вопросы задачи анализируются расчетная таблица и диаграмма.
По числам в графе y(t) находится та строка, в которой положительные числа переходят в отрицательные (на диаграмме график полета тела пересекает горизонтальную ось). Это и есть момент падения с точностью до величины шага времени. Так получается ответ на 1-й вопрос.
Ответы на остальные вопросы находятся аналогично.
Финансовая модель
Постановка задачи. В сберегательном банке имеется два вида денежных вкладов: с простым и сложным (капитализированным) процентом. Простой процент составляет 30% в год, сложный — 25% в год. Первоначальная сумма вклада составляет 1000 рублей. Каким видом вклада и в ка-кие сроки выгодно пользоваться?
План создания модели. Объектами исследования являются денежные вклады. Известны начальная сумма вклада, процентные ставки для каждого вида вкладов. Чтобы получить суммы вкладов на каждый год, будем строить таблицу сумм вкладов. Вычисления удобно производить с помощью электронных таблиц.
Построение математической модели.
Введем обозначения. Пусть S0 – начальная сумма вклада, P1 – простой процент, P2 — сложный процент, А1 — сумма вклада с простым процентом через 1 год, В1 — сумма вклада со сложным процентом через 1 год, Ai и Bi — суммы с простым и сложным процентом через i лет. Тогда имеем следующие равенства:

Соотношение вкладов с простым и сложным процентом через n лет определяется разностью An – Bn.
Если An – Bn > 0, то выгоднее пользоваться вкладом с простым процентом.
Если An – Bn < 0, то выгоднее пользоваться вкладом со сложным процентом.
Построение компьютерной модели (на рис. показан фрагмент таблицы).
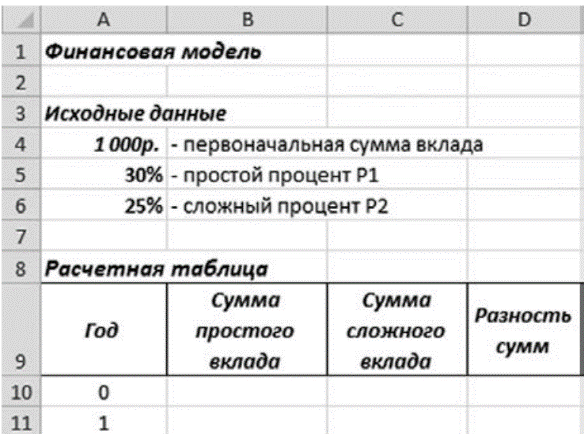
Получение решения задачи. Проанализировав разность сумм, определяем, каким вкладом выгоднее пользоваться.

Задания по теме урока
Задача 1. Создайте в Excel модель полета камня согласно описанному примеру.
Задача 2. Найдите угол бросания, при котором камень с начальной скоростью 35 м/с упадет в 100 м от места бросания. Найдите время полета.
Задача 3. Для дальности 100 м и при угле бросания 60° найдите начальную скорость и время полета камня.
Задание 4. Создайте в Excel финансовую модель и ответьте на вопросы:
- Сколько лет будет более выгоден вклад с простым процентом, чем со сложным?
- Начиная с какого года будет более выгоден вклад со сложным процентом?

Домашнее задание
§ 24 учебного пособия, ответить на вопросы
Форма отправки
Форма видна только зарегистрированным пользователям.
