Урок 22. Моделирование случайных событий. Метод Монте-Карло

Цель урока: изучить моделирование случайных событий посредством табличного процессора и языка программирования, познакомиться с методом Монте-Карло.

---

Событие — результат испытания. Различают достоверные, невозможные и случайные события,

Событие является достоверным, если в рассматриваемом испытании оно происходит всегда.

Невозможное событие — событие, которое в данном опыте не может произойти.

Например, после прыжка в воду «выйти мокрым» — достоверное событие, а «выйти сухим» — невозможное событие.

Событие называется случайным, если в результате испытания оно может произойти или не произойти. Например, выпадение герба при подбрасывании монеты, попадание «в десятку» во время стрельбы по мишени, выигрыш в лотерею.

Случайные числа — такая последовательность чисел, для которой невозможно предсказать следующее число, даже зная все предыдущие

Псевдослучайные числа обладают свойствами случайных чисел, но каждое следующее число вычисляется по заданной формуле.

В языках программирования используют псевдослучайные числа, которые получают с использованием генератора случайных чисел.

Реализация генератора случайных чисел:

Программа	Функция	Описание
Язык програм­мирования PascalABC.NET	Random(х);	Возвращает случайное целое число в диапазоне от 0 до х – 1 (х — целое число)
	Random(а, b);	Возвращает случайное целое число в диапазоне от а до b (а, b — целые числа)
	Random;	Возвращает случайное вещественное число в диапазоне [0..1)
Табличный про­цессор MS Excel	СЛЧИС()	Возвращает случайное вещественное число в диапазоне [0..1)
	СЛУЧМЕЖДУ (а; b)	Возвращает случайное целое число в диапазоне от а до b (а, b — целые числа)

Генератор случайных чисел в электронной таблице пересчитывает свои зна­чения после каждого изменения рабочей таблицы или после нажатия клавиши F9.

Под методом Монте-Карло понимается численный метод решения математических задач при помощи моде­лирования случайных величин.

Суть метода Монте-Карло рассмотрим на примере зада­чи определения площади плоской фигуры.

Пусть имеется плоская фигура, которая находится внутри пря­моугольника с известной площадью S₀.

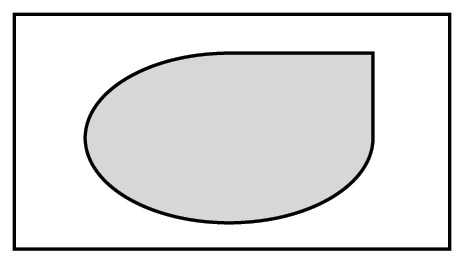
Засыплем мысленно прямоугольник тончайшим слоем песка. Если посчитать общее число n песчинок и число k тех песчинок, которые попали на фигуру, то приближенно площадь фигуры можно считать по формуле

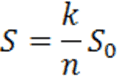
Метод Монте-Карло состоит в воспроизведении на компьютере опыта случайного разбрасывания n песчинок с использованием генератора случайных чисел и с подсчетом числа k песчинок, которые попали на фигуру.

---

Задания по теме урока

Задание 1. Пройдите тест по ссылке

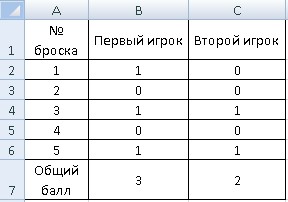
Задание 2. Создайте в табличном процессоре MS Excel модель игры «Орел или решка» для двух игроков с пятью бросаниями монеты для каждого из них.

Пусть каждый из игроков за «орла» («герб») получает 1 балл, за «решку» – 0 баллов.

1. В ячейке В2 задайте функцию, которая будет генерировать два числа – 0 или 1: =СЛУЧМЕЖДУ(0;1)
2. Скопируйте функцию из ячейки В2 на диапазон ячеек В2:С6.
3. В ячейках диапазона В7:С7 подсчитайте общее количество очков, полученных каждым из игроков.

Задание 2. Создайте в системе программирования PascalABC.NET программу, которая заполняет прямоугольник 400х300 пикселей точками случайного цвета. Количество точек – 100000.

Шаблон программы:

uses graphabc;
const n=100000;
var x,y:_________;
begin
  rectangle(___,___,___,___);
  for var i:=1 to ____ do
  begin
    x:=random(___);
    y:=random(___);
    setpixel(___,___,______);
    end;
end.

Задание 2. Создайте в табличном процессоре MS Excel модель бросания игрального кубика для двух игроков с десятью бросаниями кубика для каждого из них.

---

Домашнее задание

§ 7 электронного пособия, ответить на вопросы

---

Форма отправки

Форма видна только зарегистрированным пользователям.