Существует два подхода к измерению количества информации: содержательный и алфавитный.
Содержательный подход является субъективным, так как информация рассматривается с точки зрения конкретного человека. Количество информации в сообщении не равно нулю, если сообщение пополняет знания человека.
Алфавитный подход является объективным способом измерения информации. При таком подходе количество информации зависит не от содержания, а от объема текста (т. е. от числа знаков в тексте).
Содержательный подход к измерению информации
При содержательном подходе информацию рассматривают как знания, которыми обладает человек. Сообщение несет информацию для человека, если содержащиеся в нем сведения являются для него новыми и понятными.
Неопределенность знаний о некотором событии — это количество возможных результатов события.
Пример. Игральный кубик с шестью гранями может с равной вероятностью упасть на любую из них. Значит, неопределенность знаний о результате бросания кубика равна шести.
Единица измерения информации — это количество информации, уменьшающее неопределенность знания в два раза.
Единица измерения информации называется бит. Сообщение, уменьшающее неопределенность знаний в два раза, несет 1 бит информации.
Пример. Вы бросаете монету, загадывая, что выпадет: орел или решка. Есть всего два варианта возможного результата бросания монеты. В этом случае перед подбрасыванием монеты неопределенность знаний о результате равна двум.
После подбрасывания монеты и получения сообщения о том, что выпал, например, орел, неопределенность знаний уменьшилась в два раза: было два варианта, остался один. Значит, узнав результат бросания монеты, вы получили 1 бит информации.
Сообщение о том, что произошло одно событие из двух равновероятных, несет один бит информации.
Пусть в некотором сообщении содержатся сведения о том, что произошло одно из N равновероятных событий. Тогда количество информации i, заключенное в этом сообщении, и число событий N связаны формулой N = 2i
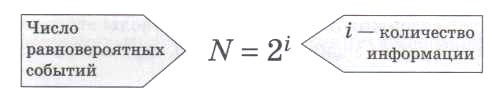
Пример. Определить, какое количество информации несет сообщение о том, что из 256 одинаковых по размеру, но разных по цвету шариков наугад выбрали зеленый шар.
Решение. 256 = 28. Значит, сообщение несет в себе 8 бит информации.
Алфавитный подход к измерению информации
Алфавитный подход основан на том, что всякое сообщение можно закодировать с помощью конечной последовательности символов некоторого алфавита.
Алфавит — упорядоченный набор символов, используемый для кодирования сообщений на некотором языке.
Любой произвольный алфавит можно заменить двоичным алфавитом.

Пример. Алфавит содержит 4 символа.
| Порядковый номер символа | 1 | 2 | 3 | 4 |
| Двоичный код | 00 | 01 | 10 | 11 |
Пример. Алфавит содержит 8 символов.
| Порядковый номер символа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Двоичный код | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
В 4-символьном алфавите с помощью двух двоичных символов закодировали 4 произвольных символа (4 = 22). В 8-символьном алфавите с помощью трех двоичных символов закодировали 8 произвольных символов (8 = 23).
В 16-символьном алфавите 16 символов можно закодировать с помощью 4 двоичных символов, так как 16 = 24. 32 символа можно закодировать с использованием 5 двоичных цифр, так как 25 = 32, и т. д.
Если алфавит содержит N символов, то символы этого алфавита можно закодировать с помощью i двоичных разрядов, где i можно получить из соотношения N = 2i.
Мощность алфавита (N) — количество символов алфавита.
Информационный вес символа (i) — количество двоичных цифр (бит), требуемое для кодирования символов этого алфавита. При этом информационный вес символа должен быть выражен целым числом.
Чтобы определить объем информации в сообщении при алфавитном подходе, нужно:
- определить информационный вес символа (i) по формуле 2i = N, где N — мощность алфавита;
- определить количество символов в сообщении (К);
- вычислить объем информации по формуле I = i * К.
количество символов в сообщении К = 100;
информационный объем сообщения I = 8* 100 = 800 бит.
Единицы измерения информации
Минимальная единица измерения информации — бит. 1 байт = 8 бит.
1 Кбайт (один килобайт) = 1024 байт;
1 Мбайт (один мегабайт) = 1024 Кбайт;
1 Гбайт (один гигабайт) = 1024 Мбайт;
1 Тб (один терабайт) = 1024 Гбайт;
1 Пб (один петабайт) = 1024 Тбайт.
Задания
Файл, с описанием заданий можно скачать по ссылке (скачать).
Форма отправки
Выполните задания, после чего отправьте вашу ЭРТ на проверку через форму ниже. Проверьте, чтобы в имени файла были указаны ваша ФАМИЛИЯ и КЛАСС.
Форма видна только зарегистрированным пользователям.
[useyourdrive dir=»1KZS9Xrck4EH5Qgtnt9h16Pns_ErntrtP» account=»116159993468290683473″ mode=»upload» viewrole=»administrator|author|contributor|editor|subscriber|guest» downloadrole=»none» upload=»1″ upload_auto_start=»0″ uploadrole=»administrator|author|contributor|editor|subscriber» ]