Цель урока: Изучить операции над множествами: пересечение, объединение.
Отношения между подмножествами можно наглядно изобразить в виде кругов Эйлера.
Пример кругов Эйлера:
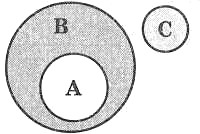
В – множество живых существ;
А – множество людей;
С – множество неодушевленных предметов.
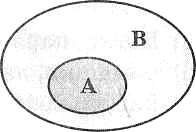
Множество А называют подмножеством множества В, если каждый элемент множества А является в то же время элементом множества В. Обозначение: А ⊂ В.
Пример: {1, 2} ⊂ {1, 2, 3, 4}.
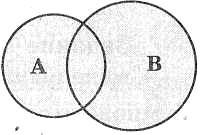
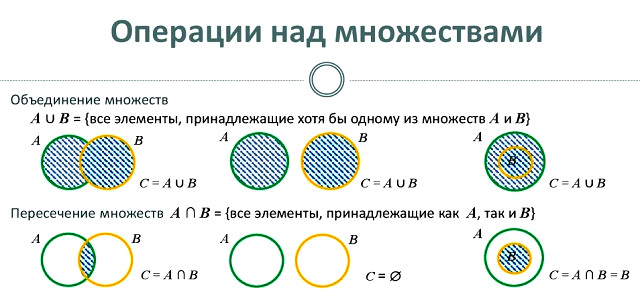
Суммой, или объединением, множеств А и В называется множество, состоящее из элементов, которые принадлежат хотя бы одному из множеств А, В.
Объединение множеств обозначают так: А ∪ В.
Пример: {1, 2, 3} ∪ {2, 3, 4} = {1, 2, 3, 4}.
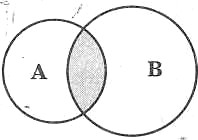
Пересечением множеств А и В называется множество, состоящее из тех и только тех элементов, которые принадлежат множествам А и В одновременно.
Пересечение множеств обозначают так: А ∩ В.
Пример: {1, 2, 3} ∩ {2, 3, 4} = {2, 3}.
Решение задач и использованием кругов Эйлера

Задания по теме урока
Задание 1. Выполните тест по ссылке
Дополнительные задания:

Домашнее задание
§ 6 учебного пособия, ответить на вопросы после параграфа.
